It is not possible that as a programmer or computer scientist, you never heard or thought about Data Structure and Algorithms. Even if you are not a programmer, you deal with them in everyday life without knowing!
For example, let’s say you bought some stuff as groceries and want to put them in your refrigerator. You definitely think about: How can I store them to access them easier when I need something?
The above simple question is always one of the most essential and challenging aspects of every computer system. Efficiency in access and process. If you are not efficient, you cost yourself, your pocket, and your company a leg and arm.
So what is exactly a data structure? what is an algorithm? how many types do they have? and how can we decide which one to choose?
I try to cover the basics for the above questions.
**Note**: These are really complex and big topics. I am just telling the basics here. If you want to go deep, I suggest taking a course or reading a book!
Let’s go!
Data Structure
Imagine you have some documents such as old bills, certifications, etc. You will access them from time to time for your paperwork. The very first question that comes to everybody’s mind is: How can I organize them?
This is basically the definition of Data Structure. How do we organize our data? The goal of any data structure is to organize the data so that we can access them efficiently when we need them.
The definition of Efficiency depends on the problem you want to solve and your goals. For instance, you might say I need my bills more often than certifications, so I put them on top of the certifications. Or, you can say I need my recent papers more so I order my papers chronologically.
In computer programming, we have different types of data structures to store the data. We can group them like this:
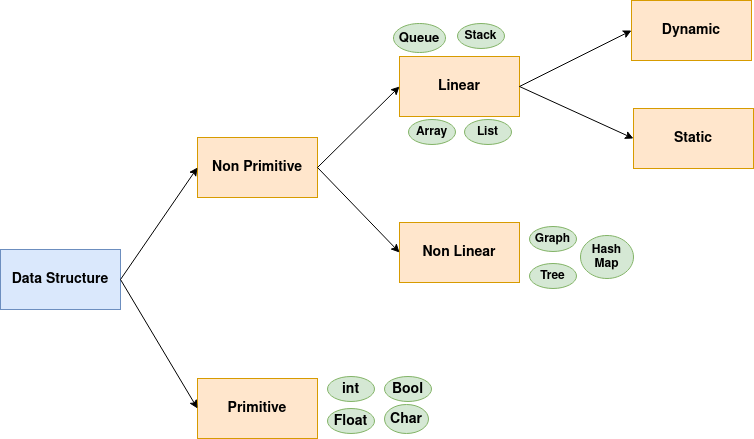
Let’s have a look at the names above:
Primitive: These are the basic data structures that are built in a programming language. These types contain only a value and have a fixed size in memory such as integer, character, and boolean. We use these types to build more complex data structures. They are often directly supported by the hardware.
Non Primitive: These are complex data structures. They are not built-in in most programming languages. Often you need to either use a library or implement them yourself. They can be linear such as arrays and queues. Or can be non-linear such as Hash maps and Graphs. Also, there are dynamic types that do not have a fixed size and can change such as Stack. Or they can be fixed and Static such as Arrays.
Algorithm
Consider you want to access the bill in your papers with the highest cost. What can you do?
In this situation, you need a formula that helps you to access the highest cost as efficiently as possible. We call this Algorithm.
Algorithms are the operations that you perform on your data structure to achieve a specific goal.
For example, finding the maximum in a list of values.
An algorithm must be:
- Correct: Leads to the expected result
- Efficient: It is not only enough to be correct. We want the answer as fast and resource-efficient as possible.
There are different groups for algorithms. But one way of seeing it is based on the way they solve a problem:
Divide and Conquer: These types of algorithms divide a complex problem into smaller ones with the same nature. The idea is by solving the small ones we reach the solution for the main problem. An example would be the Merge Sort algorithm that breaks a list into smaller ones and merges those to reach a sorted big list. The problem at hand has to be dividable (Optimal Substructure). This means the solution for small sub-problems should lead to the solution for the main problem. Otherwise, it does not work.
Dynamic programming: It works like divide and conquer. However, here we optimize our performance by remembering repetitive patterns to avoid redundant calculations (Overlapping Subproblems). For instance, in the Fibonacci problem, we can save the old answers and reuse them for the future. Let’s say we calculated Fibonacci(20). Then if we want to calculate Fibonacci(22), we can reuse the answer for Fibonacci(20) without repeating the entire calculation from scratch.
Greedy: As the name suggests, these algorithms pick the “best answer at the moment” with the hope that the best local answer will be the best global one. We also do NOT update our selected answers in the future. An example of it would be Insertion Sort where we insert an incoming element in the position that we think is the best based on the current situation.
Brute-force: This is very simple. We just try to find all possible answers and then decide which one is correct! may sound absurd, but in many problems we have to do it. For example, if you want to find all possible combinations of some words or characters
Randomized: Here we include randomness in our solution. You may say that it jeopardizes the correctness. You are right! But sometimes in the real world, efficiency is more important than 100% precision! so we tolerate some mistakes but “most of the time” works and works really efficiently! (Example: quicksort)
Decide what to pick: Big O Notation
As we saw, we have many algorithms and data structures to pick. But how can we decide what to pick? We can use the Big O Notation.
This concept measures the performance of an algorithm or solution. The performance usually depends on Time and Memory.
But what is it? The ‘O’ stands for order (we measure the order of a solution). The order is the upper bound of the cost (worst-case). Basically, we measure how much our solution consumes time and space to solve the problem in the worst-case scenario.
How does the calculation work? It measures how much the cost grows with respect to the size of the input.
For example, let’s say we have a list of members with the length of n. If the solution we design requires access to each list member once, we can say the order of the solution is linear O(n).
Generally, we have these types of orders: (fastest to slowest)
Constant O(1): When we have a fixed cost regardless of the input size. Note that the fixed cost does not have to be 1. For example, O(100) is fixed so we express it as O(1).
Logarithmic O(log n): When our solution can divide the input and process them partially. For example, in the Binary Search, we can decide which subtree to traverse based on the value comparison with the root.
Linear O(n): When cost grows at the same rate as the input. For instance, when you have a For-loop in your code to traverse the input list.
Linearithmic O(n log n): Slower than linear. We face it by using sorting algorithms such as Quick Sort.
Polynomial O(n^k): This happens in cases with multiple nested loops. K is the degree of polynomial. If the K is 2 we call it Quadratic.
Exponential O(2^n): Very costly as it is obvious!
Always look at the bottleneck
How can we say what is the order of a solution? This is important since most of the time our code comprises different parts and components. We need to look at the slowest part.
So if we have three parts:
O(n^2), O(n), O(1)
Our code order is quadratic.
O(n^2 + n + 1) == O(n^2)
Hope this will be useful. for you!
The End.

